Bernard Bolzano
Bernhard Bolzano (d. 5 Ekim 1781, Prag - ö. 18 Aralık 1848, Prag), İtalyan asıllı bir Çek filozof ve matematikçi.
Babası bir İtalyan göçmeni ve küçük bir esnaftı. Annesi de, Prag'da madeni eşya ile ilgilenen bir ailenin kızıydı. Bolzano, Prag Üniversitesi'nde, felsefe, fizik, matematik ve ilahiyat çalıştı. 1807 yılında Prag'da aynı üniversiteye din ve felsefe profesörü olarak atandı. 1816 yılına kadar bu üniversitede başarılı dersler verdi. 1816 yılında, Hristiyan kilisesince benimsenen inanç, duygu ve düşünceye ters düştüğü için, bu inançlarından dolayı suçlandı. 1820 yılındaAvusturya hükümeti Bolzano'nun bu yıkıcı ve kendileri için kırıcı olan konuşmalarından dolayı onu ülkeden uzaklaştırdı.
Bolzano, İtalya asıllı bir Çek filozofuydu. Aynı zamanda iyi bir mantıkçı ve çok iyi de bir matematikçiydi. Bolzano, 1820 yılında daha çok akılcılıkla suçlandı. Onun matematiğe dayalı bir felsefesi ve düşüncesi vardı. Bu nedenle Kant'ın idealizmine karşı çıktı. Kendisi aslında bir Katolik papazıydı. 1805 yılından sonra Prag Üniversitesi'nde din felsefesi okuttu. Matematikte, sonsuzluk ve sonsuz küçükler hesabı üzerinde çalıştı. "Sonsuzluk Üzerine Paradokslar" adlı kitabı 1851 yılında yayımlandı. Noktasal kümeler üzerine de çalışmaları olmuştur.
Bolzano'nun en acıklı yılları, 1819 ile 1825 yılları arasına rastlar. Prag Üniversitesi'nce, tam 7 yıl ders vermeme ve yayın yapmamak üzere cezalandırılır. Bu üniversitece profesörlüğü de elinden alınır. Tüm bu baskılara karşı onun yüksek kafası hiç durmadan çalışmıştır. Analizde, geometride, mantıkta, felsefede ve din üzerinde çok sayıda yayınını gerçekleştirmiştir. Bugün, analizde bildiğimiz ünlü Bolzano-Weierstrass teoremi'ni ilk kez "Fonksiyonlar" adlı kitabında o kullandı. Fakat, teoremin ispatını daha önceki çalışmalarında yaptığını ve kaynak olarak da bu çalışmasını verir. Fakat, sözü edilen bu çalışma ve kaynak bugüne kadar bulunamamıştır. Çok kullanılan ve kendisinin de çok kullandığı bir teoremin ispatının Bolzano tarafından verilmiş olması olasılığı çok fazladır. Zaten bu teoremin ispatı verilmeseydi, Bolzano tarafından bu kadar çok kullanılmazdı. Sonraki yıllarda bu teoremin ispatı tam olarak Weierstrass tarafından verilmiştir. Bu nedenle, bu teorem analizde Bolzano-Weierstrass teoremi olarak bilinir.
Bolzano'nun temel çalışmaları, sonsuzlar paradoksu üzerinedir. Bolzano'ya yayın yapma yasağı konduğu için, yaşamı sürecinde bu eserlerini ne yazık ki yayınlayamamıştır. "Sonsuzlar Paradoksları" adlı çalışması ancak onun ölümünden iki yıl sonra 1850 yılında basılmıştır. Bu çalışması, sonsuz terimli serilerin birçok özelliğini içerir. Diğer birçok matematikçide olduğu gibi yaşam sürecinde çok hırpalanan, şanssızlıklarla ve baskılarla horlanan Bolzano, 18 Aralık 1848 günü Prag'da öldü.
Bernard Bolzano's parents were Bernard Pompeius Bolzano and Maria Cecilia Maurer. His mother Maria, the daughter of a Prague merchant, was German speaking and a devout Roman Catholic. Bernard Bolzano senior, the father of the subject of this biography, was born in the north of Italy and had emigrated to Prague. He made his living as a dealer in art, but was a man of modest means. Well educated, he was also a pious Roman Catholic who showed great concern towards others. An indication of how seriously he put his beliefs into practice is the fact that he was the driving force behind the founding of an orphanage in Prague. Bernard, the subject of this biography, was born in the oldest part of the city of Prague, being the fourth of his parents twelve children. Despite the large family, Bernard and one of his brothers, Johann, were the only two to reach adulthood. His health, however, was delicate and he had to fight against respiratory problems throughout his life.
Bolzano's upbringing was a major factor in the ideas that he taught later in his life. He was much influenced by his father's active attempts to care for his fellow men, and this was strengthened by the Piarist Gymnasium that Bolzano attended in Prague between 1791 and 1796. There he was taught by the Roman Catholic followers of Joseph Calasanz who was the Spanish founder of the Ordo Clericorum Regularium Pauperum Matris Dei Scholarum Piarum (Order of Poor Clerks Regular of the Mother of God of the Pious Schools). Although Spanish, Calasanz founded Order, usually called by the name Piarists, in Rome at the beginning of the 17th century. Members of the Piarist Order were teachers who made a fourth vow to take special care of young people in addition to the usual three vows made by monks. It is fair to say that Bolzano left this environment more convinced of the moral beliefs, which had been foremost in his upbringing and in his schooling, than in the purely religious Christian beliefs.
Bolzano entered the Philosophy Faculty of the Charles University of Prague in 1796, studying philosophy, physics and mathematics. Bolzano was particularly influenced in his mathematical studies by reading Kaestner'sMathematische Anfangsgründe. Kaestner was concerned with philosophical questions in mathematics, was deeply interested in the philosophy of mathematics, and took great care to prove many results which were thought "obvious", so not requiring proof, by other mathematicians of the day. Bolzano, who soon developed a strong belief in this approach, wrote:-
My special pleasure in mathematics rested therefore particularly on its purely speculative parts, in other words I prized only that part of mathematics which was at the same time philosophy.
During the year 1799-1800 Bolzano undertook research in mathematics with Frantisek Josef Gerstner and also contemplated his future. In the autumn of 1800, against his father's wishes, he began three years of theological study at the Charles University. While pursuing his theological studies he prepared a doctoral thesis on geometry. He received his doctorate in 1804 writing a thesis giving his view of mathematics, and what constitutes a correct mathematical proof. In the preface he wrote:-
I could not be satisfied with a completely strict proof if it were not derived from concepts which the thesis to be proved contained, but rather made use of some fortuitous, alien, intermediate concept, which is always an erroneous transition to another kind.
Two days after receiving his doctorate Bolzano was ordained a Roman Catholic priest. However, as Russ points out in [50]:-
He came to realise that teaching and not ministering defined his true vocation.
In fact his years of study of theology had done nothing to strengthen his acceptance of the religious beliefs on which Christianity is founded. However, his professor at the Charles University had put forward an argument which Bolzano had found very persuasive, namely that faith in a doctrine was justified if it led to moral good. Later in his writings Bolzano argued for a more general form of this argument:-
Of all actions possible to you, choose always the one which, weighing all consequences, will most further the good of the totality, in all its parts.
This allowed Bolzano to accept the mystical elements of Christianity for the greater good of mankind, although he did not accept them to be historically true.
In order to understand the events of Bolzano's life, we need to fill in a little background about the situation in Bohemia. From early in the 17th century, after Roman Catholic forces defeated the Bohemian Protestants, Bohemia had been ruled by the Habsburgs. It was absorbed into the Austrian Empire, German became the language of instruction in grammar schools and the Charles University, and Czech nationalism was suppressed. In 1781 Joseph II granted religious tolerance but the French Revolution brought in an era of free thinking which the rulers feared. To hold the Empire together, the rulers decided to move against all nationalistic organisations which they believed encouraged ideas of independence for various parts of the Empire. In 1804, Emperor Franz who ruled from Vienna, decided that one way to counter the impact of the enlightenment was to strengthen the hold of the Roman Catholic Church which tended to be very conservative and opposed to liberal thinking. He set up chairs of philosophy of religion in the universities as one of the means to achieve his aims.
Chairs in the universities were filled by competition and Bolzano entered two such competitions for chairs at the Charles University. One was for the chair of mathematics which became vacant on the death of Stanislaw Vydra, the other being for the new chair in the philosophy of religion which Emperor Franz had just established. Bolzano came top in both competitions, but the university preferred to give him the chair in the philosophy of religion since they were then able to give the mathematics chair to Ladislaw Jandera who had substituted for Vydra during his illness between 1801 and 1804. In many ways Bolzano was exactly the wrong person to fill this chair given the reasons for its creation, for he stood for all the ideas which Franz feared, being a free thinker who believed in social justice, pacifism, and equality for the Czech speaking Bohemians.
His appointment to the chair had to be confirmed in Vienna, and they certainly understood that he was not the Roman Catholic conservative that they had been hoping would be appointed. Confirmation of his appointment was delayed while Vienna considered what its best action should be, but in 1807 it was granted [10]:-
... he lectured on religion and moral philosophy with strong pacifistic and socialistic overtones. He used the pulpit to proclaim before hundreds of impressed students a kind of utopian socialism. In his sermons he tried to prove the essential equality of all human beings, attacked private property obtained without work, and exhorted his listeners to sacrifice everything in their struggle for human rights.
The appointment of Bolzano was viewed with suspicion by the Austrian rulers in Vienna. He criticised discrimination wherever he saw it, principally by the German speaking Bohemians against their Czech fellow citizens, and also he criticised the anti-Semitism displayed by both the German and Czech Bohemians. Some members of the Roman Catholic Church were also unhappy because Bolzano's lectures contains elements of rationalism. He certainly had supporters within the Church, for example the important Archbishop of Prague and Dr Fessl who directed the seminary of Leitmeritz. In 1815 Bolzano was elected to the Royal Bohemian Society of Sciences which was bilingual society drawing its members mainly from the German speakers but also from Czech speakers. Bolzano published On the Condition of the Two Nationalities in Bohemia in 1816 in which he put into print his concerns that the Czech Bohemians were dominated by the German speaking Bohemians. The peasants were Czech speaking, the cities largely inhabited by German speakers but Bolzano saw the problems which were being created due to increasing industrialisation which saw Czech speakers moving into the cities. Bolzano's career continued to flourish, despite the fact that charges were bought against him at the Vienna court in 1816, and in 1818 he was elected Dean of the Faculty of Philosophy at Charles University.
Bolzano was suspended from his position in December 1819 after pressure from the Austrian government. In addition to being suspended from his professorship, he was put under house arrest, had his mail censored, and not allowed to publish. Between 1821 and 1825 he was tried by the Church, and despite his strong defence of his views, was required to recant his supposed heresies. He refused to do so and resigned his chair. From 1823 he had spent the summers living near the village of Techobuz in southern Bohemia, on the estate of his friends Josef and Anna Hoffmann, while he spent the winter living in Prague with his brother Johann. J J I Hoffmann was a mathematician who had reviewed several of Bolzano's earlier works (see [54]). Between 1830 and 1841 he lived throughout the year with the Hoffmanns, having much time to devote to study. When Anna Hoffmann took ill in 1841, Bolzano and the Hoffmanns moved to Prague where they all lived with Johann Bolzano (Anna died in 1842). There Bolzano again became an active member of the Royal Bohemian Society of Sciences and was president during 1842-43. He had suffered from respiratory problems for most of his life and these became more severe as he grew older. In the winter of 1848 he contracted a cold which, given the poor condition of his lungs, led to his death.
Although some of his books had to be published outside the Austrian Empire because of government censorship, he continued to write and to play an important role in the intellectual life of his country. In fact he had won a partial lifting of the publication ban, and he was only forbidden from publishing anything of a religious or political nature.
Bolzano wrote Beyträge zu einer begründeteren Darstellung der Mathematik. Erste Lieferung (1810), the first of an intended series on the foundations of mathematics. Bolzano wrote the second of his series but did not publish it. Instead he decided to:-
... make myself better known to the learned world by publishing some papers which, by their titles, would be more suited to arouse attention.
Pursuing this strategy he published Der binomische Lehrsatz ... (1816) and Rein analytischer Beweis ... (Pure Analytical Proof) (1817), which contain an attempt to free calculus from the concept of the infinitesimal. He is clear in his intention stating in the preface of the first of these that the work is:-
... a sample of a new way of developing analysis.
Although Bolzano did achieve exactly what he set out to achieve, he did not do so in the short term, his ideas only becoming well known after his death. In [50] Russ describes Bolzano's aims in the 1817 paper:-
In this work ... Bolzano ... did not wish only to purge the concepts of limit, convergence, and derivative of geometrical components and replace them by purely arithmetical concepts. He was aware of a deeper problem: the need to refine and enrich the concept of number itself.
The paper gives a proof of the intermediate value theorem with Bolzano's new approach and in the work he defined what is now called a Cauchy sequence. The concept appears in Cauchy's work four years later but it is unlikely that Cauchy had read Bolzano's work.
After 1817, Bolzano published no further mathematical works for many years. However, in 1837, he published Wissenschaftslehre , an attempt at a complete theory of science and knowledge. Between sometime before 1830 and the 1840s, Bolzano worked on a major work Grössenlehre. This attempted to put the whole of mathematics on a logical foundation was published in parts, while Bolzano hoped that his students would finish and publish the complete work. His work on paradoxes Paradoxien des Unendlichen, a study of paradoxes of the infinite, was published in 1851, three years after his death, by one of his students. The word set appears here for the first time. In this work Bolzano gives examples of 1-1 correspondences between the elements of an infinite set and the elements of a proper subset.
Most of Bolzano's works remained in manuscript and did not become noticed and therefore did not influence the development of the subject. Many of his works were not published until 1862 or later. Bolzano's theories of mathematical infinity anticipated Georg Cantor's theory of infinite sets. It is also remarkable that he gave an example of a function which is nowhere differentiable yet everywhere continuous.
Attempts to publish Bolzano's manuscripts are described in our article Bernard Bolzano's manuscripts.
As an example of the mathematics that Bolzano was working on while he was professor of the philosophy of religion, here is a description of what he recorded in his notebook Miscellanea mathematica in 1816. The description is by Dauben reviewing this material when it was first published in 1996:-
Bolzano opens this notebook of Miscellanea mathematica with notes on irrational and transcendental numbers and functions. But he was reading and recording his ideas on a host of other subjects as well, including the problem of how best to approach the proper mathematical understanding of zero; Legendre's work on surfaces, convexity, concavity, and conditions for congruity; analysis of other geometric concepts, including lengths, areas, volumes, and spheres; trigonometric formulas and spherical trigonometry; imaginary and exponential numbers; definition of the differential and discussion of the infinite and various opinions about it, as well as aspects of maxima and minima. ... Other topics covered here include various approaches to the calculus(including the method of exhaustion), and grounds for asserting the certainty of mathematics.
In addition to his mathematical work, Bolzano was important as a philosopher and as a logician. We mention briefly two major works. First there is Lehrbuch der Religionswissenschaft (Textbook of the Science of Religion) (1834) in which he bases his religious philosophy on ethics [35]:-
He criticises Kant's categorical imperative and his doctrine of postulates, and advocates a version of utilitarianism.
His second major work which we mention is Wissenschaftslehre (Theory of Science) published in four volumes in 1837. The first two volumes cover his ideas on the philosophy of logic, the third volume presents a theory of scientific discovery, while the final volume presents his methodology of writing textbooks [17]:-
Bolzano's theory of science (Wissenschaftslehre) contains a great amount of very valuable information concerning the development of logic from its beginnings in Aristotle till the post-Kantian period. In a critical exposition, Bolzano presents views of his predecessors and compares them with his own point of view.


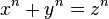


 ve
ve 
